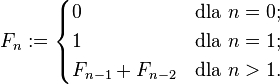Ciąg arytmetyczny – ciąg liczbowy, w którym każdy wyraz jest sumą wyrazu bezpośrednio go poprzedzającego oraz ustalonej liczby zwanej różnicą ciągu. Zwykle zakładamy, że wyrazy ciągu arytmetycznego są liczbami rzeczywistymi, choć można rozważać również ciągi arytmetyczne o wyrazach zespolonych.
Ciąg geometryczny (lub postęp geometryczny) – ciąg liczbowy (skończony bądź nieskończony), którego każdy kolejny wyraz od drugiego począwszy jest iloczynem wyrazu poprzedniego przez pewną stałą nazywaną ilorazem. Ciąg geometryczny można traktować jako multiplikatywną wersję (addytywnego) ciągu arytmetycznego.
Ciąg Fibonacciego – ciąg liczb naturalnych określony rekurencyjnie w sposób następujący:
- Pierwszy wyraz jest równy 0, drugi jest równy 1, każdy następny jest sumą dwóch poprzednich.
Formalnie:
Szereg nieskończony. Definicja szeregu: konstrukcja umożliwiająca wykonanie uogólnionego dodawania przeliczalnej liczby składników. Wyrazy szeregu często powstają w wyniku zastosowania pewnej reguły, takiej jak np. wzór czy algorytm. W przeciwieństwie do sumowania, do pełnego zrozumienia i manipulowania nimi szeregi wymagają narzędzi analizy matematycznej. Poza ich wszechobecnością w samej matematyce szeregi szeroko stosuje się w innych dyscyplinach ilościowych takich jak fizyka czy informatyka; szczególnie ważne są rozmaite szeregi funkcyjne, w tym trygonometryczne, na czele z szeregiem Fouriera czy potęgowe (za pomocą których można przybliżać z dowolną dokładnością wiele funkcji).